Geometry and Dynamics of the Solar System

by Frank Hoogerbeets — published 11 May 2023

1. Basic Universal Principle
2. Geometric Development
3. The Planets
4. Orbital Motion
5. Orbital Period
6. The gravitational constant
7. Magnetic fields

In 1766 German astronomer Johann Daniel Titius mentioned a mathematical rule that describes the mean distance or semi-major axis of the planets from the Sun. This rule was published by his colleague Johann Elert Bode in 1772 and is since known as the law of Titius and Bode. Before Titius and Bode the Scottish mathematician and astronomer David Gregorie described an approximation of this law, which was found in his text book 'The Elements of Astronomy' (1715). For a long time it was considered an emperical law and referred to as such in physics and astronomy books. Today there is a tendency among scientists to consider the Titius-Bode law a 'mathematical coincidence'. Since 2006 the science journal Icarus no longer accepts papers with new interpretations of this law.

David Gregorie

Johann Daniel Titius

Johann Elert Bode

The rule generally referred to is mathematically defined as

a = \frac{(4 + x)}{10}

whereby

x = 0, 3, 6, 12, 24, 48, 96, 192, 384

The result $a$ is the mean distance in astronomical units (AU), so $0.4$ for Mercury, $0.7$ for Venus, $1.0$ for Earth, etc.

The rule in this form is from an astronomical perspective, whereby the result is a close approximation of the actual mean distance of each planet from the Sun, expressed in AU. We usually do not see an attempt to explain this mathematical rule that adds 4 and uses a specific geometric progression from 0 to 3 to 6 to 12 etc. Why is it a progression of number 3 and why is number 4 added?

Basic Universal Principle

Everything in the Universe is cyclical, whether it is a star revolving around the centre of a galaxy, a planet around a star, a moon around a planet or an electron around an atom's nucleus. The first recognition of a cycle for life on Earth is birth and death. We see leaves born on tree branches during each Spring and die each Fall with our planet's seemingly infinite orbital motion around the Sun. A cycle is circular by definition, whereby ellipses and spirals are special cases.

From mathematics we know that in order to uniquely define a circle, three points must be known. This is not a mathematics invented by humans; it is a universal principle and here we touch on the three fundamental aspects of life that literally build cycles on all levels of existence: birth-life-death. These three aspects have been known by various names in many cultures throughout history. So is it a coincidence that we find a geometric progression specifically of number 3 in the Titius-Bode law, or is the underlying structure of the Solar System based on a universal principle?

The basic principle of the Universe is the polarity birth-death and the constant that flows through it in different forms: life. Electricity in our homes is but one example of this principle: there are two wires, one positive and one negative, which allow electrons to flow through a circuit. This polarity is known by different names: birth-death, positive-negative, active-passive, male-female to name a few. The third aspect, life, is neutral; it is neither positive nor negative, but is the result of the two. The three aspects of the Universe in total harmony are geometrically expressed by the equilateral triangle, with three angles of 60° and each aspect at equal distance from each other (figure 1).

(figure 1)

Geometric Development

Back to the Titius-Bode law, we see a progression of number 3, but a progression or development needs polarity in order to take place, because without interaction of two opposite poles nothing happens. This is true on all levels of existence. So where is the polarity in the numerical sequence? It is right at the beginning:

-3 0 3+

Obviously, action or development cannot happen at the negative pole; it happens at the positive or active pole. So the full geometric development at the core of the Titius-Bode law should have the form of sequence 1.

-3 0 3 6 12 24 48 96 192 384

(sequence 1)

This geometric progression is specific to the Solar System, but no matter the type of progression or development, the basic action is always multiplication or mirroring of the three fundamental aspects within themselves so that smaller cycles can be built within larger cycles and vice versa (figure 2).

(figure 2)

In its perfect geometric form, a mirroring of the three fundamental aspects always results in the development of 1 to 4, geometrically from one triangle to four triangles, whereby the binding of the three aspects is always preserved, both in the triangular and linear fashion. The basic principle of 4 is expressed by the four cardinal points of the Universe, usually referred to as the four wind directions, which are fixed and never change, proving their coordinating function. So the next step in this development would be the mirroring of each of the four triangles, resulting in sixteen triangles (figure 3).

(figure 3)

It is important to realize the characteristics of the numbers 1, 4, 16, 64, 256, 1024, ... as their digital roots express an infinite repetition of the numbers 1, 4, 7 without exception: (1+6=7), (6+4=10; 1+0=1), (2+5+6=13; 1+3=4), (1+0+2+4=7). The numbers 4 and 7 themselves are expressions of number 1: (1+2+3+4=10; 1+0=1), (1+2+3+4+5+6+7=28; 2+8=10; 1+0=1), so the infinite repetition 1-4-7 is essentially an expression in a more concrete form of the three aspects 1-1-1, whereby 1=positive, 4=neutral and 7=negative. In the visible electromagnetic spectrum we distinguish seven colors, three primary and four secondary. If we were to apply the same principle of adding 4 to 3, the geometric development of sequence 1 of the Titius-Bode law takes the form of sequence 2.

1 4 7 10 16 28 52 100 196 388

(sequence 2)

Every interaction of positive and negative in the Universe results in a new expression of the three fundamental aspects, whereby polarities rotate and alternate. The expression of the first interaction is 1 + 2 = 3 (figure 4). The next expression is a multiplication by the result (3) of the first polarity's interaction (figure 5), whereby the polarity rotates and alternates, meaning that positive (+) becomes neutral, negative (-) becomes positive and neutral becomes negative. This second expression of the three fundamental aspects of the Universe contains the key harmonics that build and influence electromagnetic currents and subsequently all matter. This becomes apparent with the expression of the third step, the multiplication by the result (15) of the second polarity's interaction (figure 6).

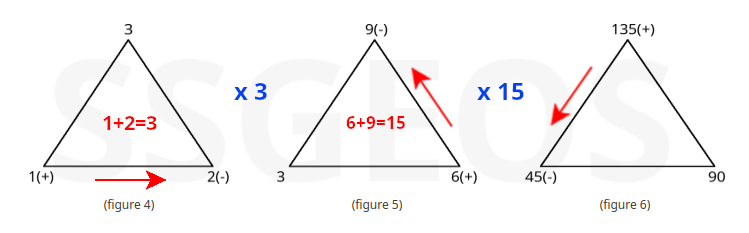
geometric development of number 3 with alternating polarity rotation

It is not a coincidence that the electric and magnetic component of the electromagnetic wave are always 90° out of phase, as 90 is the neutral aspect of the third expression. This expression defines the key geometry between the planets that results in great electromagnetic influence when Mercury and Venus are involved. Hence, it is also not a coincidence that the numbers of sequence 2 of the Titius-Bode law multiplied by the sum of the second polarity's interaction (15) closely match the observed mean distances of the planets from the Sun expressed in million kilometers (sequence 3). The very electromagnetic field of the Solar System guarantees this geometric distribution of the planets (and asteroid belts).

15 60 105 150 240 420 780 1500 2940 5820

(sequence 3)

In 1791 the metre as a fundamental unit of length was officially defined by the French Academy of Sciences as one ten-millionth of a quarter meridian, so that Earth's circumference would be 40 000 kilometers. Coincidentally, the ratio of Earth's circumference and Earth's mean distance from the Sun is 1:3750, which means that the ratio of a quarter meridian to Earth's mean distance from the Sun is 15 000.

3750 x 4 = 15 000

If a quarter meridian is defined as 10 000 km then Earth's mean distance from the Sun is 150 000 000 km.

10 000 x 15 000 = 150 000 000

Maybe it is a coincidence, or maybe this was one of the reasons why a quarter meridian was used to define the metre. We will probably never know. In any case, the second polarity's interaction 15 will turn out to be key in the next parts, right down to the gravitational constant and the Sun's mass.

The Planets

So far we have only looked at the geometric blueprint of the Solar System. But how do the planets actually relate to this geometry? If we consider sequence 3 above we can correlate the planets to the mathematical numbers and their astronomical equivalents expressed in millions of kilometers (table 1).

planet	math r	real r
-	15	-
Mercury	60	57.9
Venus	105	108.2
Earth	150	149,6
Mars	240	228.0
Ceres (asteroid belt)	420	414.0
Jupiter	780	778.5
Saturn	1500	1432.0
Uranus	2940	2867.0
Pluto (Kuiper belt)	5820	5869.7

(table 1)

The astronomical values are very close to the mathematical numbers. Even the dwarf planets Ceres and Pluto and their respective belts closely match the geometry of the Titius-Bode law. But notice the absence of Neptune. Instead of quickly drawing the conclusion that the law no longer applies beyond Uranus, we must look at the astronomical mean distance of Neptune from the Sun, which is 4515.0. Is it a random distance or does it fit the law in any way? It stands to reason that if all other planets geometrically orbit the Sun, Neptune would do so too and should be approximately halfway between its neighbors. So if Neptune is between Uranus and Pluto (the Kuiper belt) we should take the average of their respective geometric mean distance and see how it relates to Neptune's astronomical mean distance:

\frac{2940 + 5820}{2} = 4380

The number 4380 corresponds well with Neptune's observed mean distance of 4515.0. It fits sequence 3 according to its digital root and is logically divisble by 15, which gives us 292 that likewise fits the digital roots of sequence 2. Subtracting 4 gives us 288 which in turn fits sequence 1 in that it is divisible by 3.

\frac{4380}{15} = 292 292 - 4 = 288

So Neptune has taken its place approximately half way between Uranus and the Kuiper belt, which is further evidence that planets — irrespective of their mass — tend to orbit their star geometrically, enforced only by the Solar System's electromagnetic field.

In the last 20 years several objects with a hydrostatic equilibrium (meaning they are spherical) have been discovered in and beyond the Kuiper belt. It distinguishes them from asteroids, which are irregular shaped rocks. Most notably, Eris and Sedna with their highly elliptical orbits seem to originate from the Kuiper belt. Is it possible that these dwarf planets are in fact orphaned moons? If so, Ceres would have been a moon of a planet that is now the asteroid belt between Mars and Jupiter. Likewise, Pluto, Eris, Sedna and probably several more would have been moons of a planet, probably a gas giant that is now the Kuiper belt. It would certainly explain the existence of these spherical bodies, as they would have formed in the presence of a strong magnetic field of a planet, similar to how the planets were formed within the magnetic field of the Solar System. In any case, we only find dwarf planets orbiting inside or near asteroid belts in the Solar System.

In the next two parts I will demonstrate that the dynamics of the Solar System — the mean orbital velocities and periods of te planets — are geometrically defined, as they relate to the second polarity's interaction (6+9=15).

Orbital Motion

In this part I will demonstrate that the mean orbital velocity of each planet in the Solar System is geometrically determined and that this velocity is accelerated/decelerated in proportion to the orbital distance. In order to do so I will start with some basic physics.

Consider an object in orbit around a central point. This motion is defined by a contant velocity (v) and a constant acceleration (a) towards the central point (figure 7).

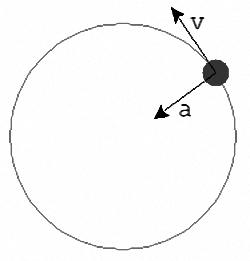
(figure 7)

This motion is inversely proportional to the distance (r) of the object to the central point:

\frac{a}{v} = \frac{v}{r}

From this we can deduce the relationship between the velocity, acceleration and mean orbital distance (formula 1).

a = \frac{v^{2}}{r}

(formula 1)

For any object in constant motion the distance (S) is defined by its velocity and the time (t) it takes to travel that distance (formula 2).

S = v \times t

(formula 2)

For an object in circular motion the distance equals the circumference:

2 π r = v \times t

Because an object in circular motion is in constant acceleration, we square to match formula 1:

4 π^{2} r^{2} = v^{2} \times t^{2}

Without external points of reference we are free to define the time it takes for a single object to complete one revolution. Therefore, we will simply define the time of one revolution as 1, in which case the velocity equals the circumference:

4 π^{2} r^{2} = v^{2}

By substituting velocity for acceleration (formula 1), we can find the constant acceleration of this object:

4 π^{2} r^{2} = a r \Rightarrow a = 4 π^{2} r

If our object were the first in a series of objects orbiting a central point, similar to the planets orbiting the Sun, then how would the velocity of each subsequent object relate to the first? Let's find out. The first object will be referred to as 1 and each subsequent object as n:

\frac{{v_{n}}^{2}}{r_{1}} = \frac{4 π^{2} {r_{1}}^{2}}{r_{n}} \Rightarrow {v_{n}}^{2} = \frac{4 π^{2} {r_{1}}^{3}}{r_{n}}

By taking the square root we can find the velocity of any object n, which is determined only by its mean orbital distance from the Sun in relationship to the mean orbital distance from the Sun of the first object (formula 3).

v_{n} = \sqrt{\frac{4 π^{2} {r_{1}}^{3}}{r_{n}}}

(formula 3)

Let's apply formula 3 to the mathematical model (sequence 3) of our Solar System that starts with the mean orbital distance 15:

v_{n} = \sqrt{\frac{4 π^{2} 15^{3}}{r_{n}}}

We can now find the mean orbital velocity of every planet by entering its mean distance from the Sun. The values are shown in table 2 along with their astronomical equivalents.

planet	math r	real r	math v	real v
-	15	-	94.25	-
Mercury	60	57.9	47.12	47.36
Venus	105	108.2	35.62	35.02
Earth	150	149.6	29.80	29.78
Mars	240	228.0	23.56	24.08
Ceres (asteroid belt)	420	414.0	17.81	17.90
Jupiter	780	778.5	13.07	13.06
Saturn	1500	1432.0	9.42	9.67
Uranus	2940	2867.0	6.73	6.79
Neptune	4380	4515.0	5.52	5.45
Pluto (Kuiper belt)	5820	5869.7	4.78	4.64

(table 2)

Note that the numerator in formula 3 is a constant. More on this later.

Orbital Period

You may recall from the part about orbital motion above that we defined the mean orbital period t for a single or first orbiting object as 1 and that by doing so we derived formula 3, which demonstrates that the mean orbital velocity of every planet is determined by its mean orbital distance from the Sun in relationship to the first mean orbital distance in the series defined by the Titus-Bode law (sequence 3). Here we will prove that this value 1 is mathematically correct, even though we already know this or formula 3 would not work.

Because we want to factor in t we go back to formula 2 squared, such that we can substitute v:

v^{2} = \frac{4 π^{2} r^{2}}{t^{2}}

Similar to what we did for velocity, we can now setup an equation that determines how the mean orbital period t of object n relates to object 1:

\frac{4 π^{2} {r_{n}}^{2}}{{t_{n}}^{2}} = \frac{4 π^{2} {r_{1}}^{3}}{r_{n}} \Rightarrow {t_{n}}^{2} = \frac{{r_{n}}^{3}}{{r_{1}}^{3}}

By taking the square root we can find the mean orbital period of any object n, which is determined only by its mean orbital distance from the Sun in relationship to the mean orbital distance from the Sun of the first object (formula 4).

t_{n} = \sqrt{\frac{{r_{n}}^{3}}{{r_{1}}^{3}}}

(formula 4)

We can apply formula 4 to the mathematical model (sequence 3) of our Solar System to determine the mean orbital period of each planet:

t_{n} = \sqrt{\frac{{r_{n}}^{3}}{15^{3}}}

The values are shown in table 3.

planet	math r	real r	math v	real v	math t
-	15	-	94.25	-	1.00
Mercury	60	57.9	47.12	47.36	8.00
Venus	105	108.2	35.62	35.02	18.52
Earth	150	149.6	29.80	29.78	31.62
Mars	240	228.0	23.56	24.08	64.00
Ceres (asteroid belt)	420	414.0	17.81	17.90	148.16
Jupiter	780	778.5	13.07	13.06	374.98
Saturn	1500	1432.0	9.42	9.67	1000.00
Uranus	2940	2867.0	6.73	6.79	2744.00
Neptune	4380	4515.0	5.52	5.45	4989.70
Pluto (Kuiper belt)	5820	5869.7	4.78	4.64	7642.71

(table 3)

We can express the mean orbital period anyway we like. For example, an observer on Earth would express the orbital period of Venus in Earth days: 31.62/18.52 = 365.24/x ⇒ x = 213.92. Because the observed mean orbital distance of Venus is slightly larger (108.2), the observed mean orbital period is slightly longer: 224.7.

The Gravitational Constant

Of the four fundamental interactions in the Universe the gravitational force is by far the weakest. At the same time it is also the most mysterious force. Even today, more than three hundred years after Newton published his Principia, the gravitational force is not well understood; scientists know how it works and how to apply the formula, but they still do not understand the gravitational force at a fundamental level. This is because the formula itself is not well understood (formula 5).

F = \frac{G M m}{r^{2}}

(formula 5)

The reason for this lack of understanding is that the formula is in fact a heuristic equation; Newton never explained why M had to be multiplied by G. In fact, we never see G and M seperately, but we do find them as a constant in Kepler's third law (formula 6).

t = \sqrt{\frac{4 π^{2} r^{3}}{G M}}

(formula 6)

But wait, when we discussed the orbital period, we saw that it only depends on the mean orbital distances (formula 4). So what is the difference between formula 4 and formula 6? It is this term:

4 π^{2}

(term 1)

This means that if we add this term to formula 4 it will give us the definition of GM:

G M = 4 π^{2} 15^{3} \Rightarrow G M = 133239.659415

(definition 1)

So even though formula 6 makes it appear as if the orbital period depends on our mysterious G and the Sun's mass M, it is in fact a geometric constant. On the NASA website this constant is defined as 132712 and adjusted to the metric system that we use (x10e+6). We found this constant also in formula 3 for the mean orbital velocity, so we can make it appear as if this velocity also depends on the two terms G and M (formula 7).

v = \sqrt{\frac{G M}{r}}

(formula 7)

The question is, why do we have two terms representing a single geometric constant? In this question lies the true mystery of the gravitational constant G. We know that it is geometric in origin because the mean velocity and period of an orbiting body in Space depend solely on its mean distance from the central body. If we look closely at the constant that GM represents, it is the result of term 1 multiplied three times by the first mean orbital distance 15 (sequence 3):

G M = 4 π^{2} \times 15 \times 15 \times 15

This first mean orbital distance is the result of sequence 2 multiplied by 15. Remember that 15 itself is the result of the second polarity's interaction (figure 5) and that the third expression (figure 6) is likewise the result of a multiplication by 15. So if any additional multiplication should occur in the geometric development of this constant as implied by G x M (definition 1), it would logically be by 15:

G M \times 15 = 4 π^{2} \times 15 \times 15 \times 15 \times 15

whereby the solar mass M is supposed to be big, which would give us the following definitions for M and G:

M = 4 π^{2} 15^{4} \Rightarrow M = 1998594.89122

(definition 2)

G = \frac{1}{15} \Rightarrow G = 0.0666666666667

(definition 3)

We can easily adjust these values to our metric system:

1998594.89122 \times 10^{24} = 1.99859489122 \times 10^{30}

0.0666666666667 \times 10^{-9} = 6.66666666667 \times 10^{-11}

Note that the sum of the exponents is again 15 (-9 + 24). We cannot escape the geometry that defines the Solar System, which is based on number 15.

Given the heuristic nature of Newton's equation (formula 5), one can only wonder how much of it is mathematically derived from the work of Kepler, who died 12 years before Newton was born. In any case, both the dynamics of the Solar System as well as the gravitational constant and the Sun's mass are the result of geometric development.

7. Magnetic Fields

While Newton's law of universal gravitation states that every object attracts every other object in the Universe, we can quickly conclude that magnetic fields dominate and can cause an opposite reaction, such as two magnets facing each others north or south pole. Indeed, the electromagnetic force is much stronger than and dominates the gravitational force. Given the fact that electricity and magnetic fields were unknown in the time of Newton and that he probably did not know that there is no gravity outside Earth's atmosphere, it is easy to understand why he compared a falling apple with the Moon orbiting Earth. But Earth's atmosphere and Space are two very different environments. In Space where astronauts float in their capsules, the Moon is actually bathing in Earth's electromagnetic field. Likewise, the planets are embedded in the electromagnetic field of the Solar System, which is transmitted and sustained by the Sun.

The key is electromagnetic radiation transmitted by a central body, such as a star or a planet. This radiation creates a field that naturally forces a revolving body to assume an orbit at a specific, geometrically determined distance, which alone determines the orbital velocity and period. This is true for any object orbiting a star or a planet, but also for every star orbiting the central mass of a galaxy or an electron orbiting the atom's core. While the electron can be pushed out of its orbit by exposing it to a certain voltage, once the exposure stops the electron reverts back to its original orbit enforced by the atom's electromagnetic field. It is not a coincidence that the formula for the electrostatic force is identical to that of the gravitational force:

F = \frac{k Q q}{r^{2}}

This is because the same geometric principles apply. No doubt these principles also exist in other solar systems. But with stars of different diameters, the geometry as well as the magnetic field strength will be proportionally different.